堆和优先权队列

堆的概念和存储表示

堆

一个大小为 n 的堆是一棵包含 n 个结点的完全二叉树，根结点为称为堆顶

1. 最小堆：树中每个结点的数据都 小于或等于 其孩子结点
   • 堆顶存储的数据最小
2. 最大堆：树中每个结点的数据都 大于或等于 其孩子结点
   • 堆顶存储的数据最大

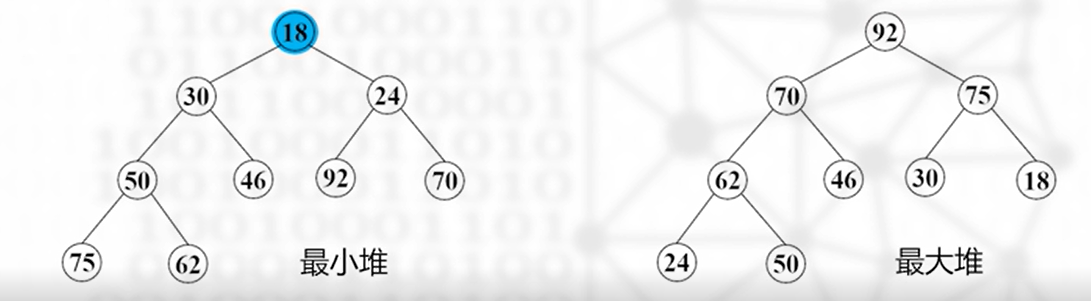
顺序表判断最小堆

#include <iostream>

int main() {
    int arr[]={2,3,11,9,10,12,14,15,13,11,12,13,18,16,17};
    for(int i=0;i<sizeof(arr)/sizeof(arr[0]);i++){
        if(arr[i]<arr[(i-1)/2]){
            std::cout<<"不是最小堆"<<std::endl;
            return 0;
        }
    }
    std::cout<<"是最小堆"<<std::endl;
    return 0;
}

建堆运算

基本思想：从最后一个叶子结点的双亲开始，一直到根结点，对不满足要求的结点依次向下调整

最后一个叶子的双亲：k_(n-2)/2

关键：

• 针对序列上的某个元素进行不断的调整，直到符合它应该处于的位置
• 当前位置处理完毕，处理当前元素调整前的前一位元素

// 建堆算法
#include <iostream>
using namespace std;

// 前向声明heapify函数
void heapify(int arr[], int n, int i);

// 构建堆的函数
void buildHeap(int arr[], int n)
{
    // 从最后一个非叶子节点开始，向上调整堆
    for (int i = n / 2 - 1; i >= 0; i--)
    {
        heapify(arr, n, i); // 调整以i为根的子树
    }
}

// 堆化函数，确保以索引i为根的子树满足堆的性质
void heapify(int arr[], int n, int i)
{
    int largest = i; // 初始化最大值为根节点
    int left = 2 * i + 1; // 左子节点索引
    int right = 2 * i + 2; // 右子节点索引

    // 如果左子节点存在且大于根节点，则更新最大值
    if (left < n && arr[left] > arr[largest])
    {
        largest = left;
    }

    // 如果右子节点存在且大于当前最大值，则更新最大值
    if (right < n && arr[right] > arr[largest])
    {
        largest = right;
    }

    // 如果最大值不是根节点，交换它们并递归堆化
    if (largest != i)
    {
        swap(arr[i], arr[largest]); // 交换根节点和最大值节点
        heapify(arr, n, largest); // 递归对受影响的子树进行堆化
    }
}

// 主函数
int main()
{
    // 初始化待构建堆的数组
    int arr[] = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1, 11};
    int n = sizeof(arr) / sizeof(arr[0]); // 计算数组大小

    buildHeap(arr, n); // 构建堆

    // 打印构建后的堆
    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " "; // 输出堆的元素
    }

    return 0; // 程序结束
}

优先权队列

特点

1. 每个元素都有一个优先权，且可以比较大小
2. 元素 按优先权的高低顺序 依次出队

传统队列

有时也可以看作优先权队列——用元素进队时间长短来表示优先权，进队时间最长，则优先权最高

方案

• 进队：将新元素放在队尾元素后，并按照 最大/小堆 进行调整 O(log₂n)
• 出队：
  • 直接取堆顶元素 O(1)
  • 然后按 最大/小堆 进行调整 O(log₂n)

%%{init: {"flowchart": {"htmlLabels": false}} }%%
flowchart LR
    a["优先权队列"]
    b["最小（或最大）堆v"]
    c["完全二叉树"]
    d["顺序存储（数组）"]
    a --> b --> c --> d
    a --> d

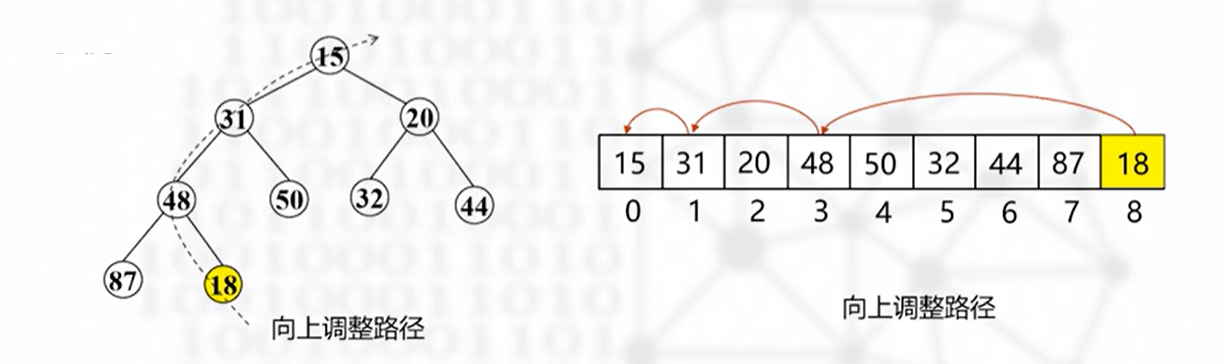
向上调整

取出优先权最高的元素

• 队列为空，直接返回
• 队列不为空，获取栈顶元素，赋值给 x
• 元素计数器减一
• 用堆尾元素替代堆顶元素
• 对新的堆顶元素执行向下调整